
Deutsch-Chinesische Enzyklopädie, 德汉百科
 IT-Times
IT-Times



 Automobile
Automobile
 ***Technology
***Technology


 IT-Times
IT-Times
 IC
IC


 IT-Times
IT-Times
 Semiconductor technology
Semiconductor technology


 IT-Times
IT-Times
 MCU
MCU

 Massachusetts-MA
Massachusetts-MA
 United States
United States

 Science and technology
Science and technology
 Global Innovators
Global Innovators


 Education and Research
Education and Research

 Education and Research
Education and Research
 *Important disciplines
*Important disciplines

 Important disciplines
Important disciplines

 Science and technology
Science and technology
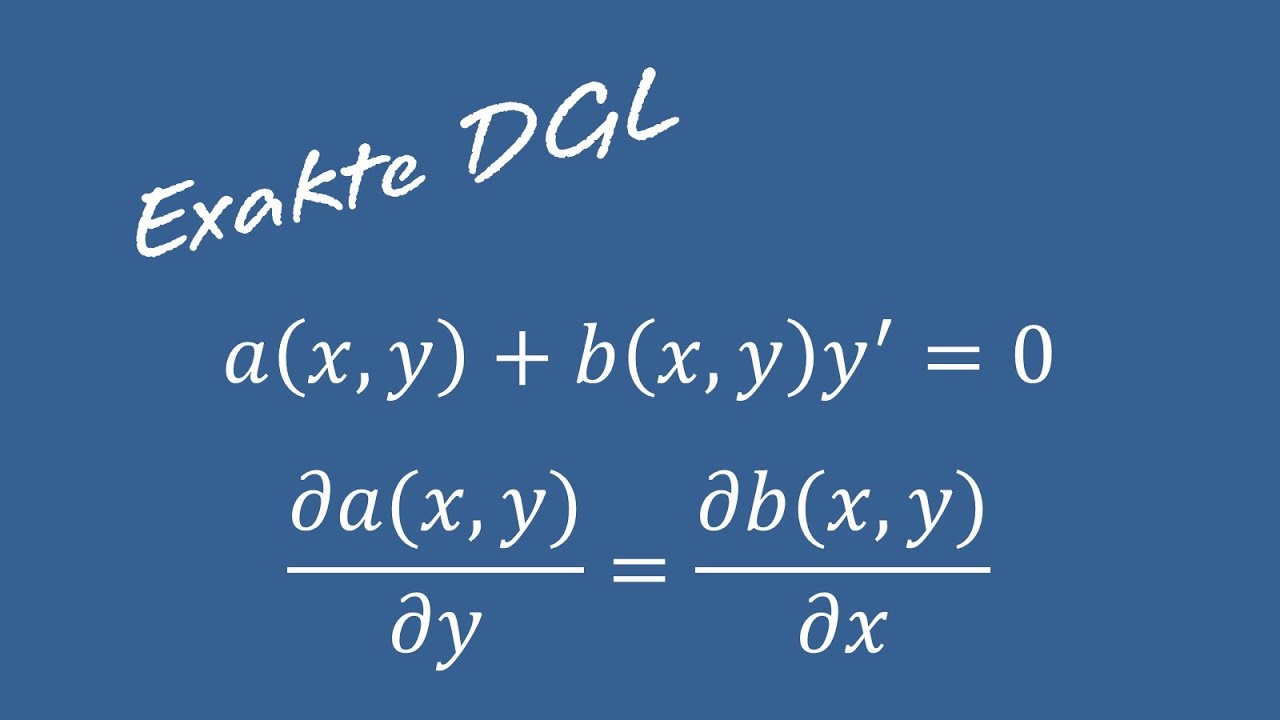
数学分析学,也称分析数学、分析学或解析学(英语:Mathematical Analysis),是普遍存在于大学数学专业的一门基础课程。大致与非数学专业学生所学的高等数学课程内容相近,但内容更加深入,一般指以微积分学、无穷级数和解析函数等的一般理论为主要内容,并包括它们的理论基础[注 1]的一个较为完整的数学学科。[1]
数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域(拓扑空间)或是有针对两对象距离的定义(度量空间),就可以用数学分析的方式进行分析。
Die Analysis [aˈnaːlyzɪs] (ανάλυσις análysis ‚Auflösung‘, ἀναλύειν analýein ‚auflösen‘) ist ein Teilgebiet der Mathematik. Als eigenständiges Teilgebiet der Mathematik existiert die Analysis seit Leonhard Euler (18. Jahrhundert). Seither ist sie die Mathematik der Natur- und Ingenieurwissenschaften.
Ihre Grundlagen wurden im 17. Jahrhundert von Gottfried Wilhelm Leibniz und Isaac Newton als Infinitesimalrechnung unabhängig voneinander entwickelt. Infinitesimalrechnung ist die mathematische Untersuchung kontinuierlicher Veränderungen, so wie Geometrie die Untersuchung der Form und Algebra die Untersuchung der Verallgemeinerung arithmetischer Operationen ist.
Zentrale Begriffe der Analysis sind die des Grenzwerts, der Folge, der Reihe sowie in besonderem Maße der Begriff der Funktion. Die Untersuchung von reellen und komplexen Funktionen hinsichtlich Stetigkeit, Differenzierbarkeit und Integrierbarkeit zählt zu den Hauptgegenständen der Analysis. Grundlegend für die gesamte Analysis sind die beiden Körper (der Körper der reellen Zahlen) und (der Körper der komplexen Zahlen) mitsamt deren geometrischen, arithmetischen, algebraischen und topologischen Eigenschaften.



 Education and Research
Education and Research

 Education and Research
Education and Research
 *Important disciplines
*Important disciplines

 Important disciplines
Important disciplines

 Science and technology
Science and technology


除了ANSI编码外,世界上还存在着另外一些对ASCII码进行扩展的编码方案,ASCII码通过扩展甚至可以编码中文、日文和韩文字符。不过令人遗憾的是,正是由于这些编码方案的存在导致了编码的混淆和不兼容性。



 Companies
Companies
 (der
(der  (der
(der  Games
Games
 Pennsylvania-PA
Pennsylvania-PA