
Deutsch-Chinesische Enzyklopädie, 德汉百科
 Bildung und Forschung
Bildung und Forschung


アレクサンダー・フォン・フンボルト財団(Die Alexander von Humboldt-Stiftung)は、国際研究協力助成を目的としてドイツ連邦共和国(西ドイツ)が1953年に設置した公益財団。名称は、博物学者のアレクサンダー・フォン・フンボルトに由来する。有能な外国人研究者に対し、ドイツにおける長期研究滞在機会を提供し、それを通じた学術文化交流を支援している。滞独研究期間中のみならず、その後の研究交流をも助成する点が、大きな特徴である。
日本からは、人文・社会科学、自然科学を問わず、毎年10-20名の奨学生が選抜され、1-2年の滞独研究を実施している。なお、2007年から、それまで設定されていた奨学生応募への年齢制限が撤廃されたため、奨学金受給の条件が大きく緩和された。
The Alexander von Humboldt Foundation (German: Alexander von Humboldt-Stiftung) is a foundation established by the government of the Federal Republic of Germany and funded by the Federal Foreign Office, the Federal Ministry of Education and Research, the Federal Ministry for Economic Cooperation and Development as well as other national and international partners; it promotes international academic cooperation between excellent scientists and scholars from Germany and from abroad.[1][2]
La Fondation Alexander von Humboldt (en allemand Alexander von Humboldt-Stiftung) est une fondation allemande pour la promotion de la coopération internationale dans le domaine de la recherche scientifique. Elle facilite des séjours de recherche de scientifiques étrangers en Allemagne, et soutient les contacts scientifiques et culturelles qui en résultent.
La Fondation finance des programmes de bourses sur concours pour des scientifiques titulaires du doctorat et particulièrement pour des séjours de recherche en Allemagne de scientifiques étrangers pour une période de six mois à deux ans. La Fondation accorde également de nombreux prix à des scientifiques de renommée mondiale comme le Prix Humboldt. Le financement est assuré par le gouvernement de la République fédérale d'Allemagne. Le siège de la fondation est à Bonn-Bad Godesberg, où la Fondation possède aussi une maison permettant d'héberger des visiteurs.
La Fondazione Alexander von Humboldt (in tedesco: Alexander von Humboldt-Stiftung) è una fondazione no-profit istituita dal governo della Repubblica Federale di Germania nel 1953.[1] Originariamente la società fu fondata a Berlino nel 1860, poco dopo la morte del naturalista Alexander von Humboldt, ma perse il suo capitale durante il periodo di iperinflazione del 1923. La fondazione fu ristabilita nel 1925 dalla Repubblica di Weimar, con l’intento di attrarre e dare supporto a studenti e accademici stranieri. Nel 1945 però, cessò di funzionare. La fondazione nella sua forma attuale fu stabilita nel 1953 dal governo di Konrad Adenauer, con il premio Nobel per la fisica Werner Heisenberg come primo presidente.[2] Oggi la Fondazione Alexander von Humboldt promuove la collaborazione tra scienziati ed accademici tedeschi ed internazionali ed è finanziata dai ministeri tedeschi degli affari esteri, dell’economia e dell’istruzione e della ricerca, oltre che ad una serie di altri enti nazionali ed internazionali.[3]
Ogni anno la fondazione assegna centinaia di premi e borse di ricerca a scienziati ed accademici stranieri che si occupano principalmente di scienze naturali, matematica e studi umanistici, e che vogliono trasferirsi in Germania per lavorare su un progetto da loro definito in cooperazione con istituti e gruppi di ricerca tedeschi.[4] I premi e le borse dalla fondazione sono tra i più prestigiosi in Germania, la quale vanta un network di oltre 28.000 ex-borsisti in 140 paesi, tra cui più di 50 premi Nobel.
Фонд Алекса́ндра фон Гумбо́льдта (нем. Alexander von Humboldt-Stiftung) — фонд, учреждённый Федеральным правительством Германии и финансируемый министерством иностранных дел Германии, министерством образования и исследований, министерством экономического сотрудничества и развития, а также другими национальными и международными партнёрами. Фонд имеет целью развитие академического сотрудничества между учёными из Германии и из других стран[1][2]. Фонд носит имя немецкого учёного Александра Гумбольдта.
Каждый год фонд на конкурсной основе присуждает более 700 исследовательских стипендий, достающихся в основном исследователям в естественных (включая математику) и гуманитарных науках[3]. В частности, среди этих стипендий есть ряд крупных премий, таких как Гумбольдтовская профессура[de] и премия Софьи Ковалевской[en]. В Германии стипендии Фонда считаются одними из самых престижных; в сообщество «выпускников» фонда входит более 26 000 гумбольдтиан в более чем 130 странах мира, включая 50 нобелевских лауреатов[4]. В России наиболее многочисленными являются клубы гумбольдтиан в Москве и в Новосибирске.

 Brandenburg
Brandenburg

 Bremen
Bremen
 Deutschland
Deutschland
 Helmholtz-Gemeinschaft Deutscher Forschungszentren
Helmholtz-Gemeinschaft Deutscher Forschungszentren
 Alfred-Wegener-Institut,AWI
Alfred-Wegener-Institut,AWI

 Schleswig-Holstein
Schleswig-Holstein

阿尔弗里德·韦格纳研究所的研究人员主要从事极地、海洋与气候方面的研究。他们希望揭示由于自然原因和人类活动所引起的地球环境系统的变化。
Das Alfred-Wegener-Institut, Helmholtz-Zentrum für Polar- und Meeresforschung (Alfred-Wegener-Institut – AWI) ist ein international anerkanntes Forschungsinstitut in Bremerhaven, das sich auf die Erforschung der Polargebiete und der ihr umgebenen Meere spezialisiert hat. Als eine von weltweit wenigen wissenschaftlichen Einrichtungen befasst es sich sowohl mit der Arktis als auch der Antarktis. Es hat in der deutschen Polarforschung eine koordinierende Rolle und befasst sich auch mit der Nordsee und den deutschen Küstenregionen. Aufgrund seiner wissenschaftlichen Ausstattung ist es in der Lage, viele Bereiche des Erdsystems von der Erdatmosphäre bis zum Ozeanboden in ihre Forschung einzubeziehen. Dabei rückt zunehmend das globale Klimageschehen in den Mittelpunkt der wissenschaftlichen Forschungsarbeit. Das Institut wurde 1980 als Stiftung des öffentlichen Rechts gegründet und ist Mitglied der Helmholtz-Gemeinschaft Deutscher Forschungszentren. Heute arbeiten an vier Standorten rund 1000 Mitarbeiter. Das Institut ist nach dem deutschen Polarforscher und Geowissenschaftler Alfred Wegener benannt.

 Bildung und Forschung
Bildung und Forschung

 Bildung und Forschung
Bildung und Forschung
 *Wichtige Disziplinen
*Wichtige Disziplinen

 Wichtige Disziplinen
Wichtige Disziplinen

 Wissenschaft und Technik
Wissenschaft und Technik


代数几何(英語:algebraic geometry)是数学的一个分支,经典代数几何研究多项式方程的零点。现代代数几何将抽象代数,尤其是交换代数,同几何学的语言和问题结合起来。
Die algebraische Geometrie ist ein Teilgebiet der Mathematik, das die abstrakte Algebra, insbesondere das Studium von kommutativen Ringen, mit der Geometrie verknüpft. Sie lässt sich kurz als das Studium der Nullstellengebilde algebraischer Gleichungen beschreiben.

 Bildung und Forschung
Bildung und Forschung

 Bildung und Forschung
Bildung und Forschung
 *Wichtige Disziplinen
*Wichtige Disziplinen

 Wichtige Disziplinen
Wichtige Disziplinen

 Wissenschaft und Technik
Wissenschaft und Technik


Die allgemeine Relativitätstheorie (![]() anhören?/i; kurz ART) beschreibt die Wechselwirkung zwischen Materie (einschließlich Feldern), Raum und Zeit. Sie deutet Gravitation als geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit. Die Grundlagen der Theorie wurden maßgeblich von Albert Einstein entwickelt, der den Kern der Theorie am 25. November 1915 der Preußischen Akademie der Wissenschaften vortrug. Zur Beschreibung der gekrümmten Raumzeit bediente er sich der Differentialgeometrie.
anhören?/i; kurz ART) beschreibt die Wechselwirkung zwischen Materie (einschließlich Feldern), Raum und Zeit. Sie deutet Gravitation als geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit. Die Grundlagen der Theorie wurden maßgeblich von Albert Einstein entwickelt, der den Kern der Theorie am 25. November 1915 der Preußischen Akademie der Wissenschaften vortrug. Zur Beschreibung der gekrümmten Raumzeit bediente er sich der Differentialgeometrie.
Die allgemeine Relativitätstheorie erweitert die spezielle Relativitätstheorie und das Newtonsche Gravitationsgesetz und geht in diese über bei hinreichend kleinen Raumzeitgebieten bzw. Massedichten und Geschwindigkeiten. In zahlreichen Tests der allgemeinen Relativitätstheorie wurde sie experimentell bestätigt und gilt in der von Einstein formulierten Form als einzige allgemein anerkannte Gravitationstheorie.
Ungeklärt ist ihre Beziehung zur Quantenphysik, dem zweiten Grundpfeiler der modernen Physik des 20. Jahrhunderts. Daher gibt es noch keine vereinheitlichte Theorie der Quantengravitation.
广义相对论是现代物理中基于相对性原理利用几何语言描述的引力理论。该理论由阿尔伯特·爱因斯坦等人自1907年开始发展,最终在1915年基本完成。[1]广义相对论将经典的牛顿万有引力定律与狭义相对论加以推广。在广义相对论中,引力被描述为时空的一种几何属性(曲率),而时空的曲率则通过爱因斯坦场方程和处于其中的物质及辐射的能量与动量联系在一起。
从广义相对论得到的部分预言和经典物理中的对应预言非常不同,尤其是有关时间流易、空间几何、自由落体的运动以及光的传播等问题,例如引力场内的时间膨胀、光的引力红移和引力时间延迟效应。广义相对论的预言至今为止已经通过了所有观测和实验的验证——广义相对论虽然并非当今描述引力的唯一理论,但却是能够与实验数据相符合的最简洁的理论。不过仍然有一些问题至今未能解决。最为基础的即是广义相对论和量子物理的定律应如何统一以形成完备并且自洽的量子引力理论。
爱因斯坦的广义相对论理论在天体物理学中有着非常重要的应用。比如它预言了某些大质量恒星终结后,会形成时空极度扭曲以至于所有物质(包括光)都无法逸出的区域,黑洞。有证据表明恒星质量黑洞以及超大质量黑洞是某些天体例如活动星系核和微类星体发射高强度辐射的直接成因。光线在引力场中的偏折会形成引力透镜现象,这使得人们可能观察到处于遥远位置的同一个天体形成的多个像。广义相对论还预言了引力波的存在。引力波已经由激光干涉引力波天文台在2015年9月直接观测到。此外,广义相对论还是现代宇宙学中的膨胀宇宙模型的理论基础。


Die amerikanische Literatur umfasst die literarische Produktion der Vereinigten Staaten und der englischen Kolonien, aus denen sie hervorgingen. Im englischsprachigen Raum ist die amerikanische Literatur Gegenstand der englischen Literaturwissenschaft, seltener der American Studies.
Im deutschsprachigen Raum, wo sich im 18. Jahrhundert der Gedanke der Nationalliteratur (Herder) und im 19. Jahrhundert der philologische Gedanke (Schlegel, Jacob und Wilhelm Grimm, Lachmann) durchsetzte, wurde für sie eine eigenständige akademische Disziplin geschaffen – die Amerikanistik.
Der überwiegende Teil der amerikanischen Literatur ist auf Englisch verfasst; dies gilt auch für die Literatur der indianischen Ureinwohner. Die in den Sprachen nicht anglophoner Einwanderer verfasste Literatur. z. B. die Chicano-Literatur, wird meist nicht im Rahmen der Amerikanistik, sondern in den entsprechenden Philologien untersucht. Zu eigenen Forschungsfeldern haben sich die „Bindestrich-Literaturen“ entwickelt, so afroamerikanische Literatur, die jüdisch-amerikanische Literatur und die chinesisch-amerikanische Literatur.
美国文学(英语:American literature 或 Literature of the United States)指在美国产生的文学(也包括建国前殖民地时期的文学作品)。用英语写成的美国文学可视为英语文学的一部分。

Die Amerikanistik ist diejenige Philologie, die sich mit der Sprache und Literatur der Vereinigten Staaten von Amerika befasst.
Das Fach existiert fast ausschließlich in Mitteleuropa, wo Autoren wie Friedrich Schlegel, Jacob Grimm, Wilhelm Grimm und Karl Lachmann im 19. Jahrhundert das Konzept der Philologie theoretisch begründet haben. Die Anhänger dieser Schule waren davon überzeugt, Texten keine echte Bedeutung entnehmen zu können, wenn sie dabei nicht in erster Linie auf die Schriftzeichen und Worte schauten.
In anderen Teilen der Welt hat die philologische Idee kaum Anhängerschaft gefunden. So sind im englischen Sprachraum Language Studies und Literature bis heute getrennte Disziplinen. Zwar existiert das Wort Americanistics im Englischen, wird aber nur verwendet, um die philologisch ausgerichtete mitteleuropäische Amerikanistik zu bezeichnen.
美国研究是研究美利坚合众国语言和文学的语言学。
19 世纪,弗里德里希-施莱格尔(Friedrich Schlegel)、雅各布-格林(Jacob Grimm)、威廉-格林(Wilhelm Grimm)和卡尔-拉赫曼(Karl Lachmann)等作家在理论上创立了语言学的概念。这一学派的追随者坚信,如果不主要研究文字和词语,就无法从文本中提取真正的意义。
在世界其他地方,语言学思想几乎无人追随。例如,在英语世界,语言研究和文学仍然是独立的学科。虽然英语中有 Americanistics(美国学)一词,但它仅用于指从语言学角度出发的中欧美国研究。
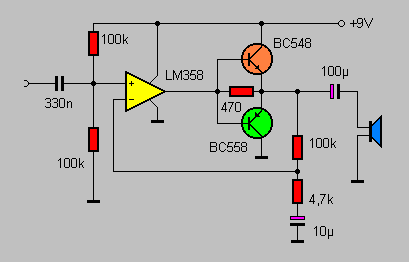
Von Analogtechnik oder analoger Technik spricht man in der Elektrotechnik und Elektronik bei sich wert- und zeitkontinuierlich ändernden physikalischen Größen, insbesondere von Spannung und Strom. Somit kann bei der Analogtechnik ein Signal in einem zeitlichen Verlauf unendlich viele Wertigkeiten besitzen. Im Gegensatz dazu betrachtet die Digitaltechnik nur diskrete Größen, also solche, die nur eine endliche, meist genau definierte Anzahl verschiedener Werte annehmen können. In der Regel benutzt man den Begriff Analogtechnik bei der Signalübertragung und -verarbeitung, aber auch im Zusammenhang mit der Mess- und Steuertechnik.
In vielen Technikbereichen wurde die Analogtechnik weitgehend durch Digitaltechnik ersetzt, allerdings bleiben meist einige Komponenten analog – zum Beispiel arbeiten beim heutzutage eigentlich volldigitalen Mobiltelefon etwa die Elektronik zur Verarbeitung der Mikrofon- und Lautsprechersignale sowie das mit Hochfrequenz arbeitende Sende- und Empfangsteil immer noch analog. In solchen Fällen, wo sich Analog- und Digitalelektronik ergänzen bzw. mischen, spricht man auch von Hybrid-Elektronik oder Mixed-Signal-Elektronik bzw. -Schaltungen.
模拟电路(英语:analogue electronics,美式:analog electronics)是涉及连续函数形式模拟信号的电子电路,与之相对的是数字电路,后者通常只关注0和1两个逻辑电平。“模拟”二字主要指电压(或电流)对于真实信号成比例的再现,它最初来源于希腊语词汇ανάλογος,意思是“成比例的”。


 Bildung und Forschung
Bildung und Forschung

 Bildung und Forschung
Bildung und Forschung
 *Wichtige Disziplinen
*Wichtige Disziplinen

 Wichtige Disziplinen
Wichtige Disziplinen

 Wissenschaft und Technik
Wissenschaft und Technik
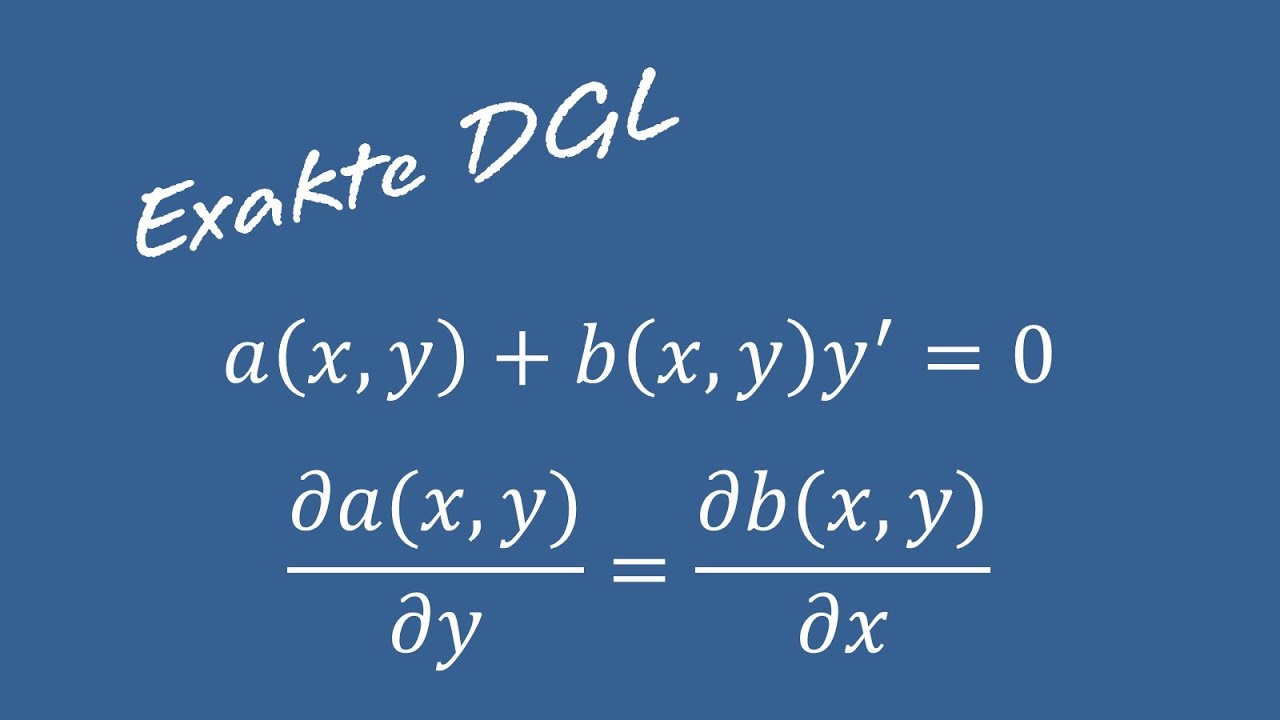
数学分析学,也称分析数学、分析学或解析学(英语:Mathematical Analysis),是普遍存在于大学数学专业的一门基础课程。大致与非数学专业学生所学的高等数学课程内容相近,但内容更加深入,一般指以微积分学、无穷级数和解析函数等的一般理论为主要内容,并包括它们的理论基础[注 1]的一个较为完整的数学学科。[1]
数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域(拓扑空间)或是有针对两对象距离的定义(度量空间),就可以用数学分析的方式进行分析。
Die Analysis [aˈnaːlyzɪs] (ανάλυσις análysis ‚Auflösung‘, ἀναλύειν analýein ‚auflösen‘) ist ein Teilgebiet der Mathematik. Als eigenständiges Teilgebiet der Mathematik existiert die Analysis seit Leonhard Euler (18. Jahrhundert). Seither ist sie die Mathematik der Natur- und Ingenieurwissenschaften.
Ihre Grundlagen wurden im 17. Jahrhundert von Gottfried Wilhelm Leibniz und Isaac Newton als Infinitesimalrechnung unabhängig voneinander entwickelt. Infinitesimalrechnung ist die mathematische Untersuchung kontinuierlicher Veränderungen, so wie Geometrie die Untersuchung der Form und Algebra die Untersuchung der Verallgemeinerung arithmetischer Operationen ist.
Zentrale Begriffe der Analysis sind die des Grenzwerts, der Folge, der Reihe sowie in besonderem Maße der Begriff der Funktion. Die Untersuchung von reellen und komplexen Funktionen hinsichtlich Stetigkeit, Differenzierbarkeit und Integrierbarkeit zählt zu den Hauptgegenständen der Analysis. Grundlegend für die gesamte Analysis sind die beiden Körper (der Körper der reellen Zahlen) und (der Körper der komplexen Zahlen) mitsamt deren geometrischen, arithmetischen, algebraischen und topologischen Eigenschaften.
 Nordrhein-Westfalen
Nordrhein-Westfalen
 IT-Times
IT-Times
 Colleges and Universities in Europe
Colleges and Universities in Europe
 Kärnten
Kärnten
 Finanz
Finanz
 (der
(der  (der
(der