
Deutsch-Chinesische Enzyklopädie, 德汉百科
 Science and technology
Science and technology


Die American Association for the Advancement of Science, auch genannt „Triple A-S“ (AAAS), ist die weltweit größte wissenschaftliche Gesellschaft und Herausgeberin mehrerer Zeitschriften, darunter Science und Science Advances. Der Leitspruch lautet „advance science and serve society“ (die Wissenschaft fördern und der Gesellschaft dienen), und der Auftrag der Gesellschaft sind der wissenschaftliche Fortschritt und weltweite Entwicklungen zugunsten der Menschheit. Sitz der Gesellschaft ist Washington, D.C.
美国科学促进会(英语:American Association for the Advancement of Science,缩写为AAAS),创建于1848年9月20日,是世界最大的非营利科学组织,下设21个专业分会,所涉包括数学、物理学、化学、天文学、地理学、生物学等自然科学学科。现有265个分支机构和1000万成员。《科学》杂志的主办者、出版者。


美国经济学会(American Economic Association,简称AEA),美国经济学者所组成的学会。建立于1885年,被认为是经济学界最重要的组织之一。它的成员主要是美国大学的经济学教授,它们所发行的学术期刊-《美国经济评论》,在经济学界极负盛名。
Die American Economic Association (AEA) ist die führende wissenschaftliche Gesellschaft für Wirtschaftswissenschaftler in den USA. Sie hat ihren Sitz in Nashville (Tennessee), USA. Den Vorsitz hat derzeit Janet Yellen (2020).[1]
Obwohl der Verein dem deutschsprachigen Verein für Socialpolitik bei der Gründung in groben Zügen nachempfunden wurde, war die AEA zunächst parteilich und nicht nur der Wissenschaft verpflichtet, was sich im Zeitverlauf jedoch schnell hin zu einer strikt wissenschaftlichen und unparteilichen Entwicklung gewandelt hat.[3] Mit 20.000 Mitgliedern (2020)[2] ist sie gleichzeitig die größte Ökonomenvereinigung der Welt.



艾姆斯研究中心(Ames Research Center)也称为美国宇航局艾姆斯,是美国宇航局位于加利福尼亚州硅谷莫菲特联邦机场的一处大型研究中心[1] 。1939年成立之初为美国国家航空咨询委员会(NACA)下辖第二实验室。1958年10月1日,该机构撤消,其资产及人员并入新成立的美国国家航空航天局。“美国宇航局艾姆斯”这一名称取自物理学家、国家航空咨询委员会创始成员之一-“约瑟夫·斯威特曼·艾姆斯”(Joseph Sweetman Ames)。据最新估计,美国宇航局艾姆斯拥有超过30亿美元资本的设备、2300名研究人员和8.6亿美元的年度预算。
艾姆斯成立之初主要专门从事螺旋桨飞机空气动力学的风洞研究,迄至今日,其研究范围已涵盖航天和信息技术领域。艾姆斯在美国宇航局的许多任务中都扮演着重要角色,在天体生物学、小型卫星、月球探测机器人、寻找宜居行星、开发超级计算机、智能/自适应系统、先进热防护以及航空天文学等方面发挥着主导作用。艾姆斯还为更安全、更高效的航空管理开发系统工具。



 Automobile
Automobile
 ***Technology
***Technology

 IT-Times
IT-Times
 IC
IC


 IT-Times
IT-Times
 Semiconductor technology
Semiconductor technology


 IT-Times
IT-Times
 MCU
MCU

 Massachusetts-MA
Massachusetts-MA
 United States
United States

 Science and technology
Science and technology
 Global Innovators
Global Innovators

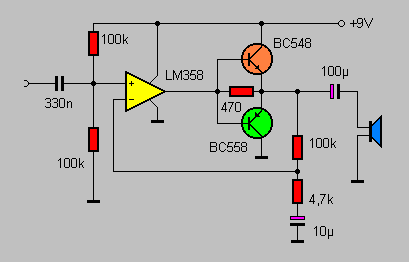
Von Analogtechnik oder analoger Technik spricht man in der Elektrotechnik und Elektronik bei sich wert- und zeitkontinuierlich ändernden physikalischen Größen, insbesondere von Spannung und Strom. Somit kann bei der Analogtechnik ein Signal in einem zeitlichen Verlauf unendlich viele Wertigkeiten besitzen. Im Gegensatz dazu betrachtet die Digitaltechnik nur diskrete Größen, also solche, die nur eine endliche, meist genau definierte Anzahl verschiedener Werte annehmen können. In der Regel benutzt man den Begriff Analogtechnik bei der Signalübertragung und -verarbeitung, aber auch im Zusammenhang mit der Mess- und Steuertechnik.
In vielen Technikbereichen wurde die Analogtechnik weitgehend durch Digitaltechnik ersetzt, allerdings bleiben meist einige Komponenten analog – zum Beispiel arbeiten beim heutzutage eigentlich volldigitalen Mobiltelefon etwa die Elektronik zur Verarbeitung der Mikrofon- und Lautsprechersignale sowie das mit Hochfrequenz arbeitende Sende- und Empfangsteil immer noch analog. In solchen Fällen, wo sich Analog- und Digitalelektronik ergänzen bzw. mischen, spricht man auch von Hybrid-Elektronik oder Mixed-Signal-Elektronik bzw. -Schaltungen.
模拟电路(英语:analogue electronics,美式:analog electronics)是涉及连续函数形式模拟信号的电子电路,与之相对的是数字电路,后者通常只关注0和1两个逻辑电平。“模拟”二字主要指电压(或电流)对于真实信号成比例的再现,它最初来源于希腊语词汇ανάλογος,意思是“成比例的”。

 Education and Research
Education and Research

 Education and Research
Education and Research
 *Important disciplines
*Important disciplines

 Important disciplines
Important disciplines

 Science and technology
Science and technology
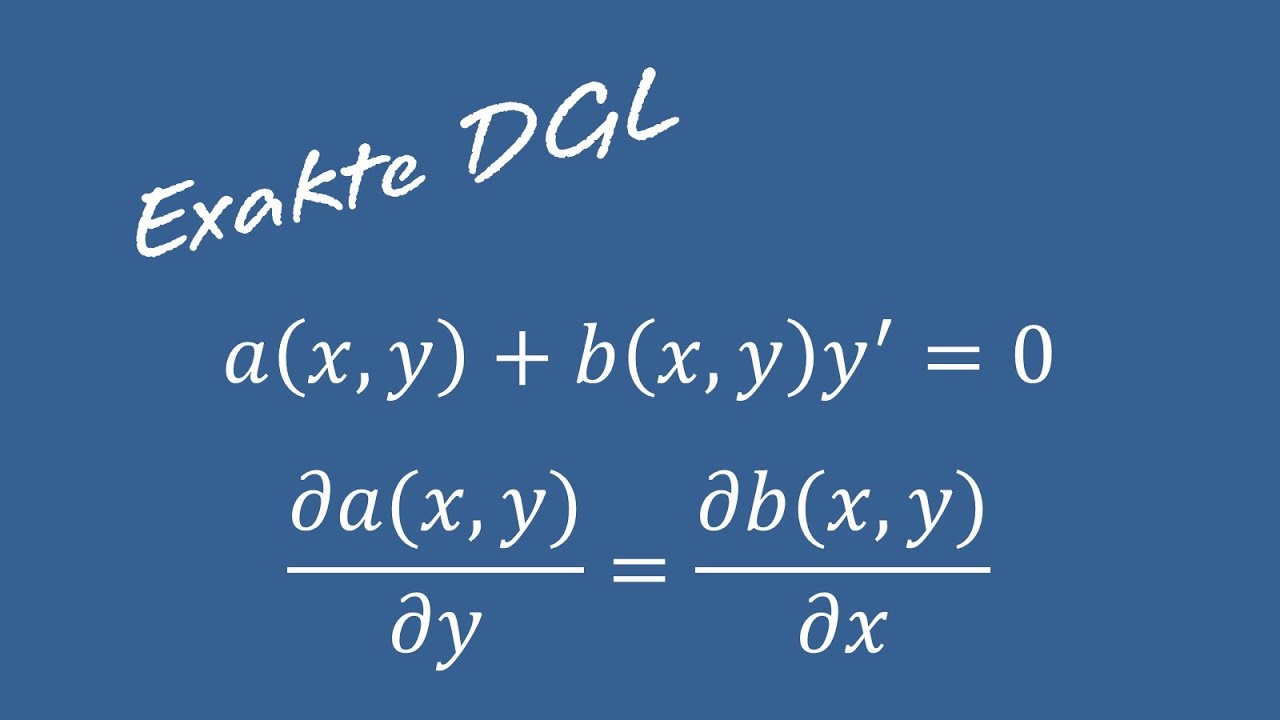
数学分析学,也称分析数学、分析学或解析学(英语:Mathematical Analysis),是普遍存在于大学数学专业的一门基础课程。大致与非数学专业学生所学的高等数学课程内容相近,但内容更加深入,一般指以微积分学、无穷级数和解析函数等的一般理论为主要内容,并包括它们的理论基础[注 1]的一个较为完整的数学学科。[1]
数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域(拓扑空间)或是有针对两对象距离的定义(度量空间),就可以用数学分析的方式进行分析。
Die Analysis [aˈnaːlyzɪs] (ανάλυσις análysis ‚Auflösung‘, ἀναλύειν analýein ‚auflösen‘) ist ein Teilgebiet der Mathematik. Als eigenständiges Teilgebiet der Mathematik existiert die Analysis seit Leonhard Euler (18. Jahrhundert). Seither ist sie die Mathematik der Natur- und Ingenieurwissenschaften.
Ihre Grundlagen wurden im 17. Jahrhundert von Gottfried Wilhelm Leibniz und Isaac Newton als Infinitesimalrechnung unabhängig voneinander entwickelt. Infinitesimalrechnung ist die mathematische Untersuchung kontinuierlicher Veränderungen, so wie Geometrie die Untersuchung der Form und Algebra die Untersuchung der Verallgemeinerung arithmetischer Operationen ist.
Zentrale Begriffe der Analysis sind die des Grenzwerts, der Folge, der Reihe sowie in besonderem Maße der Begriff der Funktion. Die Untersuchung von reellen und komplexen Funktionen hinsichtlich Stetigkeit, Differenzierbarkeit und Integrierbarkeit zählt zu den Hauptgegenständen der Analysis. Grundlegend für die gesamte Analysis sind die beiden Körper (der Körper der reellen Zahlen) und (der Körper der komplexen Zahlen) mitsamt deren geometrischen, arithmetischen, algebraischen und topologischen Eigenschaften.
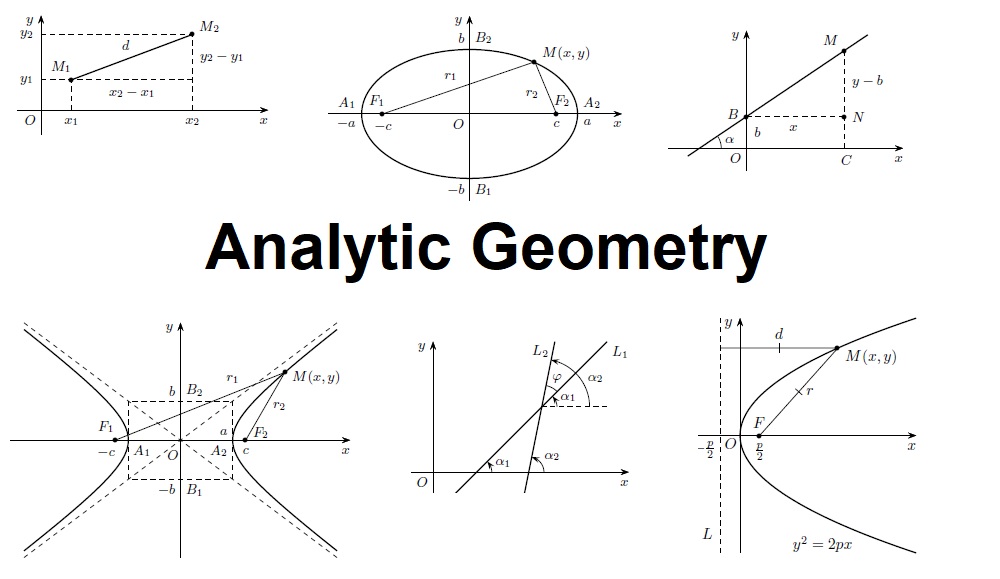
Die analytische Geometrie (auch Vektorgeometrie) ist ein Teilgebiet der Geometrie, das algebraische Hilfsmittel (vor allem aus der linearen Algebra) zur Lösung geometrischer Probleme bereitstellt. Sie ermöglicht es in vielen Fällen, geometrische Aufgabenstellungen rein rechnerisch zu lösen, ohne die Anschauung zu Hilfe zu nehmen.
Demgegenüber wird Geometrie, die ihre Sätze ohne Bezug zu einem Zahlensystem auf einer axiomatischen Grundlage begründet, als synthetische Geometrie bezeichnet.
Die Verfahren der analytischen Geometrie werden in allen Naturwissenschaften angewendet, vor allem aber in der Physik, wie zum Beispiel bei der Beschreibung von Planetenbahnen. Ursprünglich befasste sich die analytische Geometrie nur mit Fragestellungen der ebenen und der räumlichen (euklidischen) Geometrie. Im allgemeinen Sinn jedoch beschreibt die analytische Geometrie affine Räume beliebiger Dimension über beliebigen Körpern.
解析几何(英语:Analytic geometry),又称为坐标几何(英语:Coordinate geometry)或卡氏几何(英语:Cartesian geometry),早先被叫作笛卡尔几何,是一种借助于解析式进行图形研究的几何学分支。解析几何通常使用二维的平面直角坐标系研究直线、圆、圆锥曲线、摆线、星形线等各种一般平面曲线,使用三维的空间直角坐标系来研究平面、球等各种一般空间曲面,同时研究它们的方程,并定义一些图形的概念和参数。
在中学课本中,解析几何被简单地解释为:采用数值的方法来定义几何形状,并从中提取数值的信息。然而,这种数值的输出可能是一个方程或者是一种几何形状。
1637年,笛卡尔在《方法论》的附录“几何”中提出了解析几何的基本方法。 以哲学观点写成的这部法语著作为后来牛顿和莱布尼茨各自提出微积分学提供了基础。
对代数几何学者来说,解析几何也指(实或者复)流形,或者更广义地通过一些复变量(或实变量)的解析函数为零而定义的解析空间理论。这一理论非常接近代数几何,特别是通过让-皮埃尔·塞尔在《代数几何和解析几何》领域的工作。这是一个比代数几何更大的领域,不过也可以使用类似的方法。

Die Anatomie (dem Erkenntnisgewinn dienende ‚Zergliederung‘ von tierischen und menschlichen Körpern; aus altgriechisch ἀνά aná, deutsch ‚auf‘, und τομή tomḗ, deutsch ‚das Schneiden, der Schnitt‘) ist ein Teilgebiet der Morphologie und in der Medizin bzw. Humanbiologie (Anthropotomie), Zoologie (Zootomie) und Botanik (Phytotomie) die Lehre vom Bau der Organismen. Es werden Gestalt, Lage und Struktur von Körperteilen, Organen, Geweben oder Zellen betrachtet. Die pathologische Anatomie befasst sich mit krankhaft veränderten Körperteilen. Die mikroskopische Anatomie befasst sich mit den feineren biologischen Strukturen bis zur molekularen Ebene und knüpft an die Molekularbiologie an. Die klassische Anatomie verwendet eine standardisierte Nomenklatur, die auf der lateinischen und der griechischen Sprache basiert.
Ein mit der Anatomie befasster Arzt oder Naturwissenschaftler ist ein Anatom.
Der Begriff Anatomie wird schon seit dem frühen 16. Jahrhundert (auch als anatomei[A 1]) auch allgemeiner und übertragen verwendet in der Bedeutung „Zergliederung, Strukturbestimmung, Analyse von konkreten und abstrakten Dingen“, auch „Struktur, (Auf-)bau“, z. B. Anatomie des Bodens, der Kunst, der Gedanken, der Gesellschaft.
解剖学(英语:Anatomy)是涉及生命体的结构和组织的生物学分支学科[1]。解剖学和胚胎学、比较解剖学、进化生物学和系统发育有密切关系[2],而这些也可以看出解剖结构在即时(胚胎学)和长期(演化)时间尺度下的变化。人体解剖学是医学的基础学科之一[3]。
解剖学也可以分为微观尺度及巨观尺度。巨观尺度的解剖学为大体解剖学,是用肉眼来观察动物的身体及器官。大体解剖学也包括表面解剖学,而其他的部位常利用剖割的方法来进行研究。显微镜解剖学是用光学仪器(如显微镜)来研究组织(组织学)、细胞及胞器。
解剖学史的特点是对人体结构及器官功能的渐进式了解。其方法也有很大的进展,从一早期检验动物及人的尸体,到二十世纪的医学成像技术,包括X射线,但超音波和核磁共振成像技术。
解剖学和生理学都是研究器官以及各部分的结构及机能,因此很自然的会用综合学科研究法进行研究。
如果解剖学单指人体解剖学,这时候解剖学会依照各器官系统性地分类,而不是依部位来陈述。每篇解剖学的文章首先包括一个器官或系统。例如:神经、动脉、心脏等的结构描述,根据在人体找到什么而定。就此而论,解剖学文章有双重目的;首先,提供关于结构的足够资料,令文章在生理学、外科、内科和病理学方面均有可謮性;第二,给非专家的查询者或在某门科学分支上工作的人提供建立解剖学的现代科学基础的主要理论。

Anatomische Pathologie (Commonwealth) oder anatomische Pathologie (USA) ist ein medizinisches Fachgebiet, das sich mit der Diagnose von Krankheiten auf der Grundlage der makroskopischen, mikroskopischen, biochemischen, immunologischen und molekularen Untersuchung von Organen und Geweben befasst. Im Laufe des 20. Jahrhunderts hat sich die chirurgische Pathologie enorm weiterentwickelt: von der historischen Untersuchung ganzer Körper (Autopsie) zu einer modernisierten Praxis, die sich auf die Diagnose und Prognose von Krebs konzentriert, um die Behandlungsentscheidungen in der Onkologie zu unterstützen. Ihr moderner Begründer war der italienische Wissenschaftler Giovan Battista Morgagni aus Forlì.
 Universities in the USA
Universities in the USA


 Aerospace
Aerospace
 Economy and trade
Economy and trade
 Financial
Financial
 Tennessee-TN
Tennessee-TN
 Iowa-IA
Iowa-IA
 California-CA
California-CA
 Companies
Companies
 (der
(der  (der
(der  Medical, Pharmaceutical, Rehabilitation
Medical, Pharmaceutical, Rehabilitation