
Deutsch-Chinesische Enzyklopädie, 德汉百科
 法兰西岛
法兰西岛

凡爾賽宮 凡尔赛宫/Château de Versailles
Das Schloss Versailles (französisch Château de Versailles) in der gleichnamigen Nachbarstadt von Paris ist eine der größten Palastanlagen Europas und war von der Mitte des 17. Jahrhunderts bis zum Ausbruch der Französischen Revolution die Hauptresidenz der Könige von Frankreich. Der Barockbau, dessen größte Ausdehnung mehr als einen halben Kilometer beträgt, gilt als ein Höhepunkt europäischer Palastarchitektur und diente vom 17. bis zum 19. Jahrhundert als Vorbild
施耐德電子 施耐德电子
Schneider Electric SE ist ein französischer, börsennotierter Elektrotechnik-Konzern, der auf den Gebieten elektrische Energieverteilung und industrielle Automation tätig ist. Das Unternehmen hat seinen Sitz in Rueil-Malmaison bei Paris und ist in mehr als 100 Ländern vertreten.
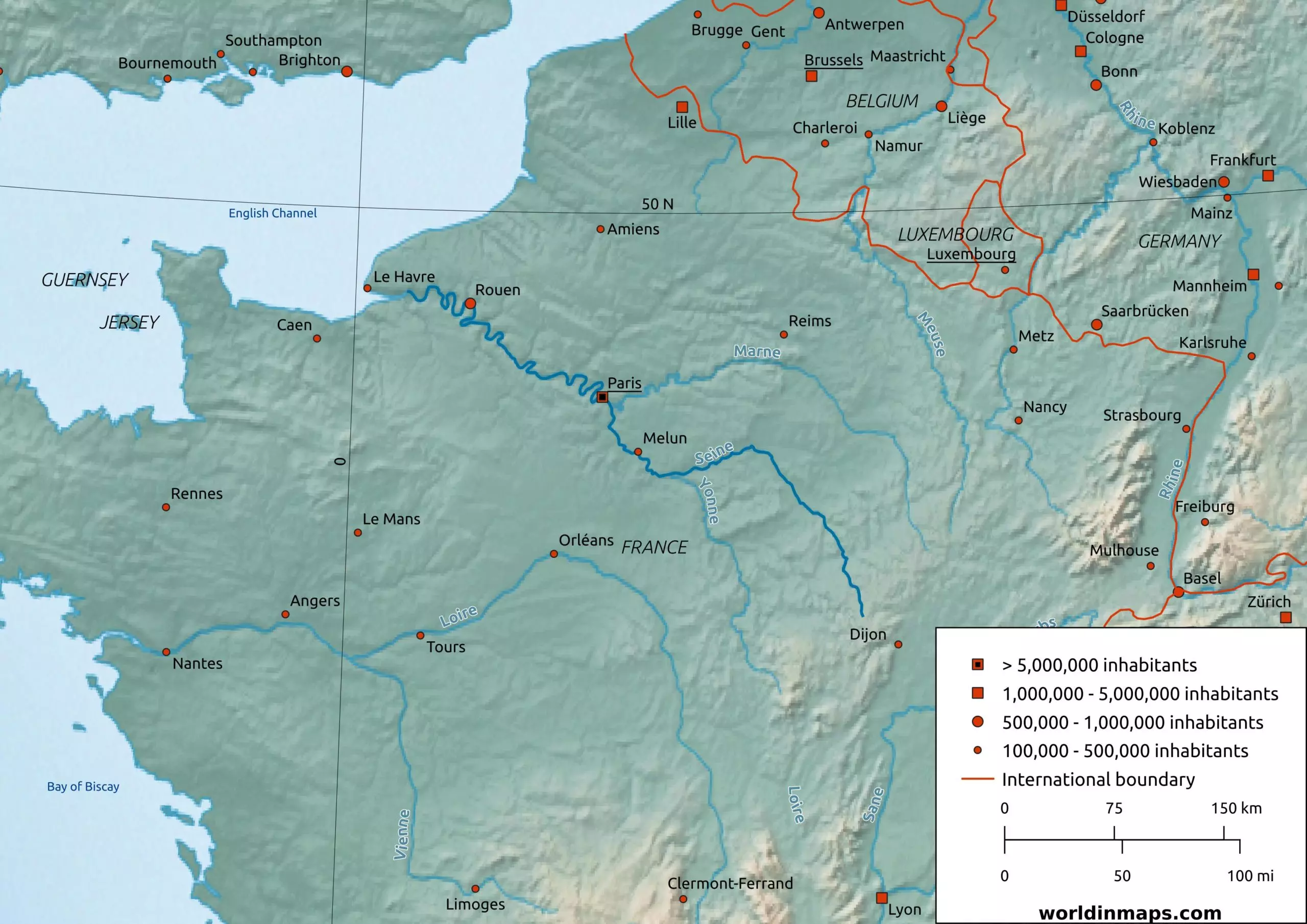
塞納河 塞纳河
Die Seine ist ein Fluss in Nordfrankreich. Sie entspringt in der Region Bourgogne-Franche-Comté, fließt von Osten nach Westen und mündet bei Le Havre in den Ärmelkanal. Mit rund 775 Kilometern Länge ist sie einer der längsten Flüsse Frankreichs.
法國興業銀行 法国兴业银行
1864, Die Société Générale, abgekürzt SG oder SocGén, mit Sitz in Paris ist eine der wichtigsten Geschäftsbanken Frankreichs, Die Großbank ist eine der Banken, die vom Financial Stability Board (FSB) auf der Liste global systemrelevanter Banken als systemisch bedeutsames Finanzinstitut eingestuft wurden. Sie unterliegt damit einer besonderen Überwachung und strengeren Anforderungen an die Ausstattung mit Eigenkapital.
法國數學學會 法国数学学会
Die Société mathématique de France (SMF) ist die französische Mathematikergesellschaft. Die Société mathématique de France wurde 1872 von Michel Chasles (dem ersten Präsidenten) gegründet und 1888 staatlich anerkannt (sie sind eine gemeinnützige Gesellschaft in der Rechtsform der Association loi de 1901). In ihren im ersten Band des Bulletin de la SMF veröffentlichten Statuten erklären sie die Förderung der Wissenschaften und der Reinen und Angewandten Mathematik zu ihrem Ziel.
 建筑艺术
建筑艺术




 企业
企业

 地理
地理


 美食家
美食家






