空气动力学（英语：Aerodynamics），是流体力学与气体动力学的一个分支，主要研究物体在空气中运动时所产生的各种力。空气动力学与气体动力学常常混用，但后者研究的气体不局限于空气。

• 空气动力学为流体力学在工程上的应用力学，特别讨论在马赫数大于0.3的流场情形。

• 空气动力学因为讨论的状况接近真实流体，考虑了真实流体的黏滞性、可压缩性、三维运动等特点，所以得到的计算方程式比较复杂，通常为非线性的偏微分方程式形式。这种方程在绝大多数的情况下都难以求得解析解的，加之早期计算技术还比较落后，所以当时大多是以实验的方式来求得所需的数据。

• 随着计算机技术的迅速发展，使用计算机进行大量数值运算来求解空气动力学方程式成为可能。利用数值法以及计算流体力学方法，可以求出非线性偏微分方程的数值解，得到所需要的各种数据，从而省去了大量的实验成本。由于数学模型的不断完善以及计算机计算能力的不断提高，现在已经可以采用电脑模拟流场的方式来取代部分空气动力学实验。

Aerodynamik (von altgriechisch ἀήρ aer, Luft, und δύναµις dynamis, Kraft) ist Teil der Fluiddynamik (Strömungslehre) und beschreibt das Verhalten von Körpern in Luft oder kompressiblen Gasen, bei letzteren spricht man auch von Gasdynamik. Das zweite Teilgebiet der Fluiddynamik, die Hydrodynamik, behandelt dagegen Flüssigkeiten.

Die Aerodynamik beschreibt die Kräfte, wie den dynamischen Auftrieb, die es beispielsweise Flugzeugen ermöglichen, zu fliegen oder Segelschiffen, mit Hilfe des Windes durchs Wasser zu segeln. Viele weitere Bereiche der Technik, wie zum Beispiel das Bauingenieurwesen oder der Fahrzeugbau, müssen sich mit der Aerodynamik auseinandersetzen.

Die Aeronomie (gesprochen A-eronomie) ist die Physik der oberen Atmosphäre oder Hochatmosphäre.

Während die Physik der unteren Atmosphäre seit Aristoteles als Meteorologie bezeichnet wird, wurde der Name Aeronomie für die Bereiche der oberen Atmosphäre erst 1954 auf der Tagung der Internationalen Union für Geodäsie und Geophysik (IUGG) in Rom festgelegt.

Die Aeronomie ist ein Teilgebiet der Geophysik. Manchmal wird die Aeronomie auch als Teilgebiet der Meteorologie zugerechnet, andere Male von dieser ausgeschlossen. Dies hängt davon ab, ob mit „Meteorologie“ nur die Meteorologie im engeren Sinne gemeint ist, also die bereits erwähnte Physik der unteren Atmosphäre, oder sich allgemeiner auf die Physik der gesamten Erdatmosphäre bezieht.

大气物理学是物理学于大气科学的应用。大气物理学家利用流体方程式、化学模型，并研究辐射收支以及大气中的能量转换（包含与其它系统间的关联，例如海洋），建立起地球及其他星球的大气模型。为了要建立起天气模型，大气物理学家使用一些与物理相关的数学理论，包含散射理论、波传递的模型、云物理学、统计物理学和空间分析。大气物理学不仅与气象学和气候学有紧密关系，更包含了研究大气所需要仪器的设计和制造，以及其数据的分析，像是遥测。在太空时代的来临及探空火箭的诞生后，高层大气物理学成为大气物理学的一个分支学科，主要研究高层大气分子的解离和游离。

Die Akustik (von griechisch ἀκούειν (ausgesprochen: „akuein“) ‚hören‘ bzw. akoustikós, ‚das Gehör betreffend‘) ist die Lehre vom Schall und seiner Ausbreitung. Im Wissenschaftsgebiet sind eine Vielzahl damit zusammenhängender Gesichtspunkte enthalten, so die Entstehung und Erzeugung, die Ausbreitung, die Beeinflussung und die Analyse von Schall, seine Wahrnehmung durch das Gehör und die Wirkung auf Menschen und Tiere. Akustik ist ein interdisziplinäres Fachgebiet, das auf Erkenntnissen aus zahlreichen Fachgebieten aufbaut, unter anderem der Physik, der Psychologie, der Nachrichtentechnik und der Materialwissenschaft. Akustik wird auch (unscharf) in drei Teilgebiete unterteilt:^[1]

• Die physikalische Akustik (oft auch nur als „Akustik“ bezeichnet) umfasst insbesondere Teilgebiete der klassischen Mechanik,
• die physiologische Akustik behandelt Schallaufnahme und Schallübertragung in den Gehörorganen und
• die psychologische Akustik die Umsetzung der akustischen Nervenreizung in die Hörempfindung.

Zu den wichtigsten Anwendungen der Akustik gehören die Erforschung und Minderung von Lärm, das Bemühen, einen Wohlklang hervorzurufen oder eine akustische Information, etwa einen Ton, zu übertragen. Außerdem ist der Einsatz von Schall zur Diagnose oder zu technischen Zwecken eine wichtige Anwendung der Akustik.

声学是物理学中波动学的一个领域，研究媒质中机械波，包括声波、超声波和次声波。研究课题包括声波的产生，接收，转换和声波的各种效应。同时声学测量技术是一种重要的测量技术，有着广泛的应用。

代数几何（英語：algebraic geometry）是数学的一个分支，经典代数几何研究多项式方程的零点。现代代数几何将抽象代数，尤其是交换代数，同几何学的语言和问题结合起来。

Die algebraische Geometrie ist ein Teilgebiet der Mathematik, das die abstrakte Algebra, insbesondere das Studium von kommutativen Ringen, mit der Geometrie verknüpft. Sie lässt sich kurz als das Studium der Nullstellengebilde algebraischer Gleichungen beschreiben.

Die allgemeine Relativitätstheorie ( anhören^?/i; kurz ART) beschreibt die Wechselwirkung zwischen Materie (einschließlich Feldern), Raum und Zeit. Sie deutet Gravitation als geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit. Die Grundlagen der Theorie wurden maßgeblich von Albert Einstein entwickelt, der den Kern der Theorie am 25. November 1915 der Preußischen Akademie der Wissenschaften vortrug. Zur Beschreibung der gekrümmten Raumzeit bediente er sich der Differentialgeometrie.

Die allgemeine Relativitätstheorie erweitert die spezielle Relativitätstheorie und das Newtonsche Gravitationsgesetz und geht in diese über bei hinreichend kleinen Raumzeitgebieten bzw. Massedichten und Geschwindigkeiten. In zahlreichen Tests der allgemeinen Relativitätstheorie wurde sie experimentell bestätigt und gilt in der von Einstein formulierten Form als einzige allgemein anerkannte Gravitationstheorie.

Ungeklärt ist ihre Beziehung zur Quantenphysik, dem zweiten Grundpfeiler der modernen Physik des 20. Jahrhunderts. Daher gibt es noch keine vereinheitlichte Theorie der Quantengravitation.

广义相对论是现代物理中基于相对性原理利用几何语言描述的引力理论。该理论由阿尔伯特·爱因斯坦等人自1907年开始发展，最终在1915年基本完成。^[1]广义相对论将经典的牛顿万有引力定律与狭义相对论加以推广。在广义相对论中，引力被描述为时空的一种几何属性（曲率），而时空的曲率则通过爱因斯坦场方程和处于其中的物质及辐射的能量与动量联系在一起。

从广义相对论得到的部分预言和经典物理中的对应预言非常不同，尤其是有关时间流易、空间几何、自由落体的运动以及光的传播等问题，例如引力场内的时间膨胀、光的引力红移和引力时间延迟效应。广义相对论的预言至今为止已经通过了所有观测和实验的验证——广义相对论虽然并非当今描述引力的唯一理论，但却是能够与实验数据相符合的最简洁的理论。不过仍然有一些问题至今未能解决。最为基础的即是广义相对论和量子物理的定律应如何统一以形成完备并且自洽的量子引力理论。

爱因斯坦的广义相对论理论在天体物理学中有着非常重要的应用。比如它预言了某些大质量恒星终结后，会形成时空极度扭曲以至于所有物质（包括光）都无法逸出的区域，黑洞。有证据表明恒星质量黑洞以及超大质量黑洞是某些天体例如活动星系核和微类星体发射高强度辐射的直接成因。光线在引力场中的偏折会形成引力透镜现象，这使得人们可能观察到处于遥远位置的同一个天体形成的多个像。广义相对论还预言了引力波的存在。引力波已经由激光干涉引力波天文台在2015年9月直接观测到。此外，广义相对论还是现代宇宙学中的膨胀宇宙模型的理论基础。

Die amerikanische Literatur umfasst die literarische Produktion der Vereinigten Staaten und der englischen Kolonien, aus denen sie hervorgingen. Im englischsprachigen Raum ist die amerikanische Literatur Gegenstand der englischen Literaturwissenschaft, seltener der American Studies.

Im deutschsprachigen Raum, wo sich im 18. Jahrhundert der Gedanke der Nationalliteratur (Herder) und im 19. Jahrhundert der philologische Gedanke (Schlegel, Jacob und Wilhelm Grimm, Lachmann) durchsetzte, wurde für sie eine eigenständige akademische Disziplin geschaffen – die Amerikanistik.

Der überwiegende Teil der amerikanischen Literatur ist auf Englisch verfasst; dies gilt auch für die Literatur der indianischen Ureinwohner. Die in den Sprachen nicht anglophoner Einwanderer verfasste Literatur. z. B. die Chicano-Literatur, wird meist nicht im Rahmen der Amerikanistik, sondern in den entsprechenden Philologien untersucht. Zu eigenen Forschungsfeldern haben sich die „Bindestrich-Literaturen“ entwickelt, so afroamerikanische Literatur, die jüdisch-amerikanische Literatur und die chinesisch-amerikanische Literatur.

美国文学（英语：American literature 或 Literature of the United States）指在美国产生的文学（也包括建国前殖民地时期的文学作品）。用英语写成的美国文学可视为英语文学的一部分。

Die Amerikanistik ist diejenige Philologie, die sich mit der Sprache und Literatur der Vereinigten Staaten von Amerika befasst.

Das Fach existiert fast ausschließlich in Mitteleuropa, wo Autoren wie Friedrich Schlegel, Jacob Grimm, Wilhelm Grimm und Karl Lachmann im 19. Jahrhundert das Konzept der Philologie theoretisch begründet haben. Die Anhänger dieser Schule waren davon überzeugt, Texten keine echte Bedeutung entnehmen zu können, wenn sie dabei nicht in erster Linie auf die Schriftzeichen und Worte schauten.

In anderen Teilen der Welt hat die philologische Idee kaum Anhängerschaft gefunden. So sind im englischen Sprachraum Language Studies und Literature bis heute getrennte Disziplinen. Zwar existiert das Wort Americanistics im Englischen, wird aber nur verwendet, um die philologisch ausgerichtete mitteleuropäische Amerikanistik zu bezeichnen.

美国研究是研究美利坚合众国语言和文学的语言学。

19 世纪，弗里德里希-施莱格尔（Friedrich Schlegel）、雅各布-格林（Jacob Grimm）、威廉-格林（Wilhelm Grimm）和卡尔-拉赫曼（Karl Lachmann）等作家在理论上创立了语言学的概念。这一学派的追随者坚信，如果不主要研究文字和词语，就无法从文本中提取真正的意义。

在世界其他地方，语言学思想几乎无人追随。例如，在英语世界，语言研究和文学仍然是独立的学科。虽然英语中有 Americanistics（美国学）一词，但它仅用于指从语言学角度出发的中欧美国研究。

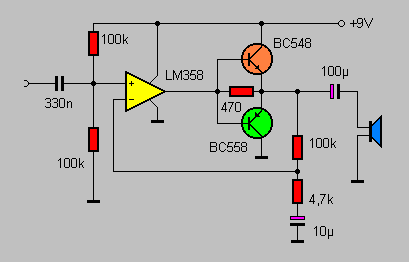
Von Analogtechnik oder analoger Technik spricht man in der Elektrotechnik und Elektronik bei sich wert- und zeitkontinuierlich ändernden physikalischen Größen, insbesondere von Spannung und Strom. Somit kann bei der Analogtechnik ein Signal in einem zeitlichen Verlauf unendlich viele Wertigkeiten besitzen. Im Gegensatz dazu betrachtet die Digitaltechnik nur diskrete Größen, also solche, die nur eine endliche, meist genau definierte Anzahl verschiedener Werte annehmen können. In der Regel benutzt man den Begriff Analogtechnik bei der Signalübertragung und -verarbeitung, aber auch im Zusammenhang mit der Mess- und Steuertechnik.

In vielen Technikbereichen wurde die Analogtechnik weitgehend durch Digitaltechnik ersetzt, allerdings bleiben meist einige Komponenten analog – zum Beispiel arbeiten beim heutzutage eigentlich volldigitalen Mobiltelefon etwa die Elektronik zur Verarbeitung der Mikrofon- und Lautsprechersignale sowie das mit Hochfrequenz arbeitende Sende- und Empfangsteil immer noch analog. In solchen Fällen, wo sich Analog- und Digitalelektronik ergänzen bzw. mischen, spricht man auch von Hybrid-Elektronik oder Mixed-Signal-Elektronik bzw. -Schaltungen.

模拟电路（英语：analogue electronics，美式：analog electronics）是涉及连续函数形式模拟信号的电子电路，与之相对的是数字电路，后者通常只关注0和1两个逻辑电平。“模拟”二字主要指电压（或电流）对于真实信号成比例的再现，它最初来源于希腊语词汇ανάλογος，意思是“成比例的”。

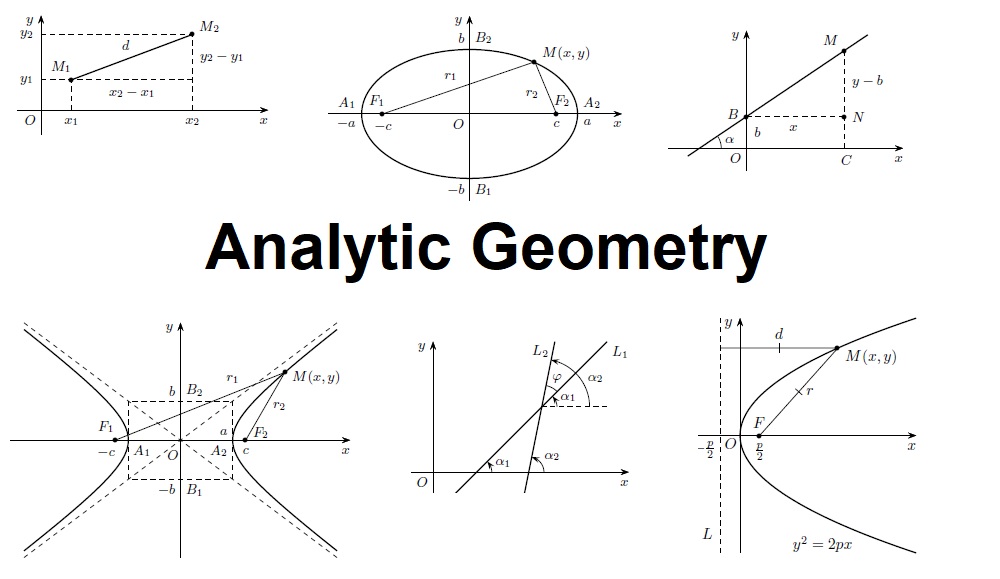
Die analytische Geometrie (auch Vektorgeometrie) ist ein Teilgebiet der Geometrie, das algebraische Hilfsmittel (vor allem aus der linearen Algebra) zur Lösung geometrischer Probleme bereitstellt. Sie ermöglicht es in vielen Fällen, geometrische Aufgabenstellungen rein rechnerisch zu lösen, ohne die Anschauung zu Hilfe zu nehmen.

Demgegenüber wird Geometrie, die ihre Sätze ohne Bezug zu einem Zahlensystem auf einer axiomatischen Grundlage begründet, als synthetische Geometrie bezeichnet.

Die Verfahren der analytischen Geometrie werden in allen Naturwissenschaften angewendet, vor allem aber in der Physik, wie zum Beispiel bei der Beschreibung von Planetenbahnen. Ursprünglich befasste sich die analytische Geometrie nur mit Fragestellungen der ebenen und der räumlichen (euklidischen) Geometrie. Im allgemeinen Sinn jedoch beschreibt die analytische Geometrie affine Räume beliebiger Dimension über beliebigen Körpern.

解析几何（英语：Analytic geometry），又称为坐标几何（英语：Coordinate geometry）或卡氏几何（英语：Cartesian geometry），早先被叫作笛卡尔几何，是一种借助于解析式进行图形研究的几何学分支。解析几何通常使用二维的平面直角坐标系研究直线、圆、圆锥曲线、摆线、星形线等各种一般平面曲线，使用三维的空间直角坐标系来研究平面、球等各种一般空间曲面，同时研究它们的方程，并定义一些图形的概念和参数。

在中学课本中，解析几何被简单地解释为：采用数值的方法来定义几何形状，并从中提取数值的信息。然而，这种数值的输出可能是一个方程或者是一种几何形状。

1637年，笛卡尔在《方法论》的附录“几何”中提出了解析几何的基本方法。 以哲学观点写成的这部法语著作为后来牛顿和莱布尼茨各自提出微积分学提供了基础。

对代数几何学者来说，解析几何也指（实或者复）流形，或者更广义地通过一些复变量（或实变量）的解析函数为零而定义的解析空间理论。这一理论非常接近代数几何，特别是通过让-皮埃尔·塞尔在《代数几何和解析几何》领域的工作。这是一个比代数几何更大的领域，不过也可以使用类似的方法。