Deutsch-Chinesische Enzyklopädie, 德汉百科
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Wichtige Disziplinen
Wissenschaft und Technik
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Wichtige Disziplinen
Wissenschaft und Technik
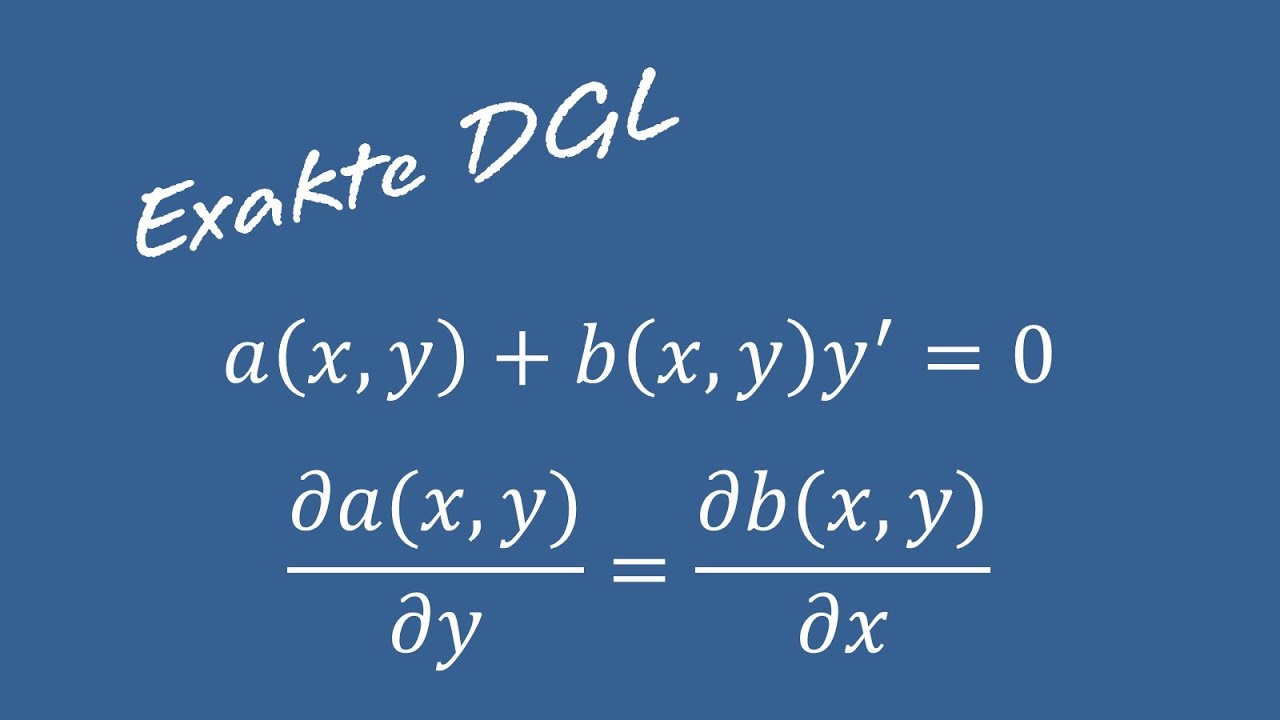
数学分析学，也称分析数学、分析学或解析学（英语：Mathematical Analysis），是普遍存在于大学数学专业的一门基础课程。大致与非数学专业学生所学的高等数学课程内容相近，但内容更加深入，一般指以微积分学、无穷级数和解析函数等的一般理论为主要内容，并包括它们的理论基础[注 1]的一个较为完整的数学学科。[1]
数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来，在微积分发展至现代阶段中，从应用中的方法总结升华为一类综合性分析方法，且初等微积分中也包括许多数学分析的基础概念及技巧，可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关，不过只要任一数学空间有定义邻域（拓扑空间）或是有针对两对象距离的定义（度量空间），就可以用数学分析的方式进行分析。
Die Analysis [aˈnaːlyzɪs] (ανάλυσις análysis ‚Auflösung‘, ἀναλύειν analýein ‚auflösen‘) ist ein Teilgebiet der Mathematik. Als eigenständiges Teilgebiet der Mathematik existiert die Analysis seit Leonhard Euler (18. Jahrhundert). Seither ist sie die Mathematik der Natur- und Ingenieurwissenschaften.
Ihre Grundlagen wurden im 17. Jahrhundert von Gottfried Wilhelm Leibniz und Isaac Newton als Infinitesimalrechnung unabhängig voneinander entwickelt. Infinitesimalrechnung ist die mathematische Untersuchung kontinuierlicher Veränderungen, so wie Geometrie die Untersuchung der Form und Algebra die Untersuchung der Verallgemeinerung arithmetischer Operationen ist.
Zentrale Begriffe der Analysis sind die des Grenzwerts, der Folge, der Reihe sowie in besonderem Maße der Begriff der Funktion. Die Untersuchung von reellen und komplexen Funktionen hinsichtlich Stetigkeit, Differenzierbarkeit und Integrierbarkeit zählt zu den Hauptgegenständen der Analysis. Grundlegend für die gesamte Analysis sind die beiden Körper (der Körper der reellen Zahlen) und (der Körper der komplexen Zahlen) mitsamt deren geometrischen, arithmetischen, algebraischen und topologischen Eigenschaften.
(der 
(der
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Wichtige Disziplinen
Wissenschaft und Technik
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Geschichte
N 2000 - 2100 nach Christus
IT-Times
ComputeralgebrasystemundMathematik
Wichtige Disziplinen
Wissenschaft und Technik
Technologiekonzepte
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Wichtige Disziplinen
Wissenschaft und Technik
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Wichtige Disziplinen
Wissenschaft und Technik
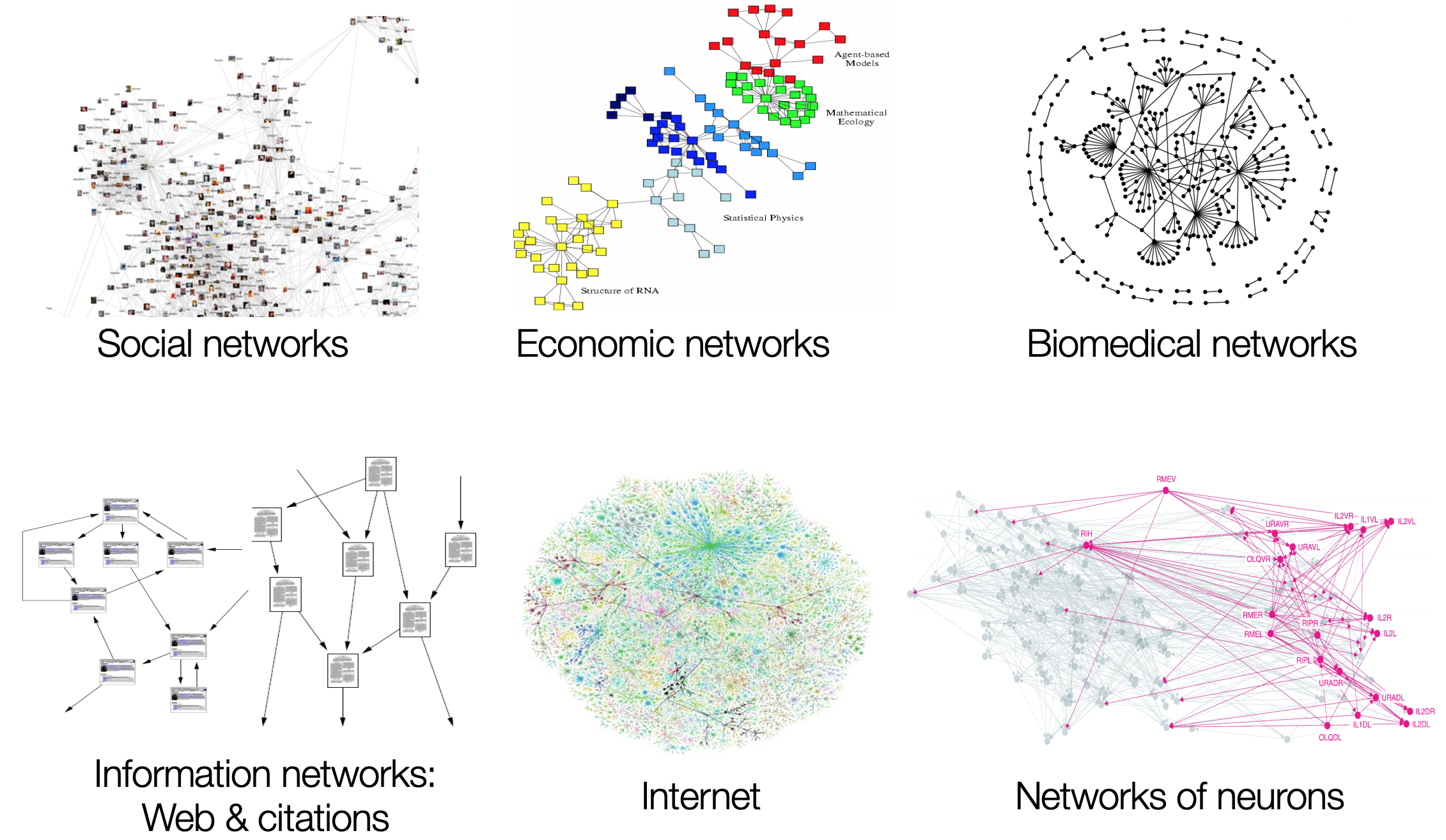
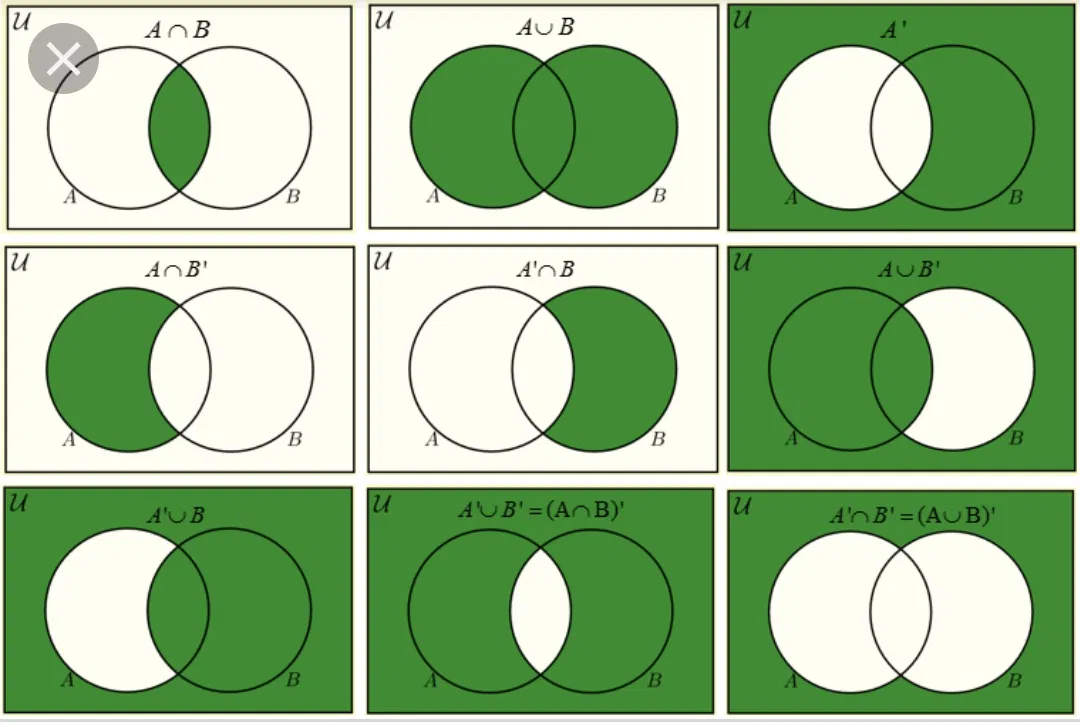
广义的组合数学（英语：Combinatorics）相当于离散数学，狭义的组合数学是组合计数、图论、代数结构、数理逻辑等的总称。但这只是不同学者在叫法上的区别。总之，组合数学是一门研究可数或离散对象的科学。随着计算机科学日益发展，组合数学的重要性也日渐凸显，因为计算机科学的核心内容是使用算法处理离散数据。
狭义的组合数学主要研究满足一定条件的组态（也称组合模型）的存在、计数以及构造等方面的问题。组合数学的主要内容有组合计数、组合设计(Combinatorial design)、组合矩阵(Combinatorial matrix theory)、组合最佳化（最佳组合）等。
Die Kombinatorik ist eine Teildisziplin der Mathematik, die sich mit endlichen oder abzählbar unendlichen diskreten Strukturen beschäftigt und deshalb auch dem Oberbegriff Diskrete Mathematik zugerechnet wird. Beispiele sind Graphen (Graphentheorie), teilgeordnete Mengen wie Verbände, Matroide, kombinatorische Designs, lateinische Quadrate, Parkettierungen, Permutationen von Objekten, Partitionen. Die Abgrenzung zu anderen Teilgebieten der Diskreten Mathematik ist fließend. Eine Definition von George Pólya bezeichnet die Kombinatorik als Untersuchung des Abzählens, der Existenz und Konstruktion von Konfigurationen.[1]
Je nach den verwendeten Methoden und Gegenständen unterscheidet man auch Teildisziplinen wie algebraische Kombinatorik, analytische Kombinatorik, geometrische und topologische Kombinatorik, probabilistische Kombinatorik, Kombinatorische Spieltheorie, Ramseytheorie. Speziell mit der Optimierung diskreter Strukturen beschäftigt sich die kombinatorische Optimierung.
Bildung und Forschung
Bildung und Forschung
*Wichtige Disziplinen
Wichtige Disziplinen
Wissenschaft und Technik
